Financial Processing > Standard Transaction E-Docs

Internal Billing

>>>>

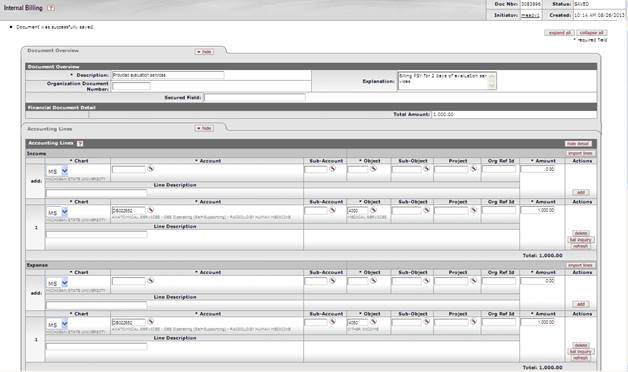
The Internal Billing (IB) document is used to bill for goods or services provided by one university department to another university department, reflecting income to the provider and expense to the customer.

     This document is not used to record the transfer of capital equipment between university accounts. Normally this type of transaction is recorded via a Transfer of Funds (TF) document.

More:

Document Layout

Process Overview

Example

Document Layout

An IB document has its own unique tab called Items in addition to the standard financial transaction tabs.

     For information about the standard tabs such as Document Overview, Notes and Attachments, Ad Hoc Recipients, Route Log, Accounting Lines, Accounting Lines for Capitalization, Create Capital Assets and Modify Capital Asset tabs, see Standard Tabs under Overview > KFS E-Doc Fundamentals.

Items Tab

The Items tab is optional; however, if you choose to use this tab, Quantity and Item Cost are required fields. This tab does not have any impact on the Accounting Lines tab, nor does it need to balance to the accounting lines. Therefore, filling out the Items tab does not automatically update the total of the accounting lines.

Items tab definition

Title	Description
Date	Optional. Enter the date of service or select it from the calendar .
Stock #	Optional. Enter the stock number for the goods or services provided.
Description	Optional. Enter the description of goods or services.
Quantity	Required. Enter the quantity of goods or services provided.
UOM	Optional. Enter the unit of measure.
Item Cost	Required. Enter the cost per item for goods or services.
Total	Display-only. The extended cost is calculated when you click add to add the line.

Process Overview

More:

Business Rules

Routing

Initiating an Internal Billing Document

Business Rules

· Negative accounting line amounts are allowed.

· There must be at least one accounting line in the Income section and one accounting line in the Expense section.

· The total in the Income section must equal the total in the Expense section in the Accounting Lines tab.

· The KFS automatically generates cash and fund balance object code offset entries as defined by the information entered into the document.

· The Account field has the following restrictions:

Sub fund group code restrictions for IB documents

Sub Fund Group Code	Description	Restriction
GC	GEN CMP - Cash Management Program	Unallowable
GD	GEN Dean Contingency	Unallowable
GP	GEN Summer School	Unallowable

Sub fund group code restrictions by Object Type for IB documents

Sub Fund Group Code	Object Type	Description	Restriction
IN	GP	GEN Summer School	Unallowable
	GA	GEN Operations	Unallowable
	GC	GEN CMP - Cash Management Program	Unallowable
	GD	GEN Dean Contingency	Unallowable
	GL	GEN TLE - Teaching Learning Environment	Unallowable
	GR	GEN Research	Unallowable
	GS	GEN Specials	Unallowable
	GT	GEN Outreach	Unallowable
	GU	GEN University	Unallowable
	RA	ERF MAES	Unallowable
	RE	ERF MSUE	Unallowable
EX	DU	DES Undistributed Gains and Losses	Unallowable
	NB	END Unrestricted Funds Functioning End	Unallowable
	NC	END Charitable Remainder Trust	Unallowable
	NE	END Unrestricted Term End Principal	Unallowable
	NG	END Unrestricted True End Principal	Unallowable
	NM	END Restricted Term Endowments Principal	Unallowable
	NR	END Restricted Funds Functioning End	Unallowable
	NU	END Undistributed Gains and Losses	Unallowable
	NX	END Restricted True Endowments Principal	Unallowable
	RU	ERF Undistributed Gains and Losses	Unallowable

The Object Code field has the following restrictions:

• Contracts and Grants Sponsored Programs object level codes are not allowed.

• Capital object codes may not be used on an Income line in the document.

Object type code restrictions for Internal Billing documents

Object Type Code	Description	Restrictions
IN	INCOME-CASH	Allowable
EE	EXPENDITURE NOT EXPENSE	Allowable
EX	EXPENSE EXPENDITURE	Allowable

Object code sub type restrictions for Internal Billing documents

Object Type Code	Description	Restrictions
BU	Budget-Only Object Code	Unallowable
CP	Construction Process	Unallowable
FR	Fringe Benefits	Unallowable
GI	Gifts	Unallowable
HW	Hourly Wages	Unallowable
IV	Investments	Unallowable
MT	Mandatory Transfers	Unallowable
PL	Capital Assets	Unallowable
RE	Reserves	Unallowable
SA	Salary and Wages	Unallowable
ST	State Appropriations	Unallowable
TF	Transfer of Funds	Unallowable
TN	TRANSFERS – GENERIC	Unallowable
WO	Write-Off Expenses	Unallowable

Routing

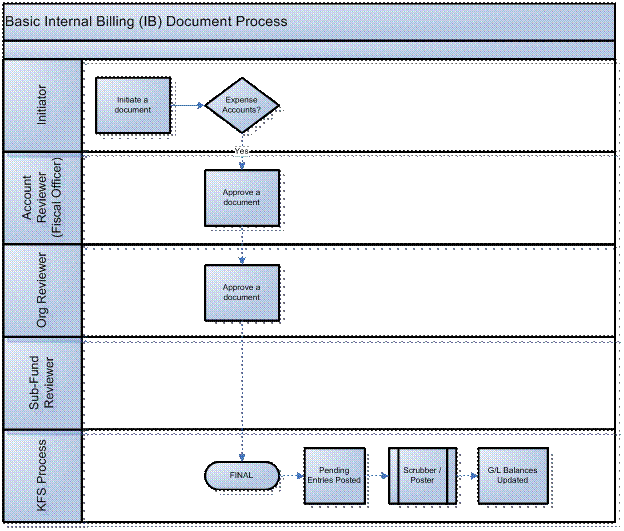
The IB document routes based on the account numbers used on the document as follows:

• The fiscal officer for each expense account must approve. See note below.

• Organization review routing occurs for the organization that owns each account.

• Sub-fund routing occurs based on the sub-fund of each account.

· The Accounting Office will need to approve the document.

If grant funds are involved the document will need approval from Contract and Grants.The document status becomes 'FINAL' when the required approvals are obtained and the transaction is posted to the G/L during the next G/L batch process.

     The IB document does not route to the fiscal officer for Income accounts on the Income side of the document.

Initiating an Internal Billing Document

1.     Select Internal Billing from the Financial Transactions submenu group.

2.     Log into the KFS as necessary.

A blank IB document with a new document ID appears.

3.     Complete the standard tabs.

     For information about the standard tabs such as Document Overview, Notes and Attachments, Ad Hoc Recipients, Route Log, Accounting Lines, Accounting Lines for Capitalization, Create Capital Assets and Modify Capital Asset tabs, see Standard Tabs under Overview > KFS E-Doc Fundamentals.

4.     If entering an Internal Billing transaction for a capital asset

Either enter the appropriate existing asset number in the Modify Capital Asset tab or enter a new asset number in the Create Capital Assets tab.

5.     Complete the Items tab (optional).

6.     Click .

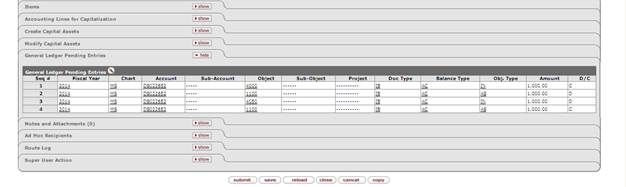
7.     Review the General Ledger Pending Entries tab.

Accounts in the Income section are credited when the amount is positive, and debited when the amount is negative. Accounts in the Expense section are debited when the amount is positive, and credited when the amount is negative. This document automatically generates cash offset entries to cash or fund balance object codes.

8.     Review the Route Log tab.

The document is routed to the fiscal officer for each expense account used in the Accounting Lines tab. The Route Status shows 'ENROUTE'.

     For information about the Route Log tab, see Route Log.

9.     Appropriate fiscal officers and organization reviewers approve the document.

     For more information about how to approve a document, see Workflow Action Buttons.

Example

The Psychology department provided evaluation services for two days to the Dean Arts and Sciences department and needs to bill for these services.

The income of $300.00 is recorded to the Evaluation and Testing object code 5023 on the Psychology account 1031400, and the expense of $300.00 is charged to the Evaluation object code 5024 on the Dean and Sciences account 1023200.

The IB document provides a simple mechanism for departments to charge one another for services rendered.